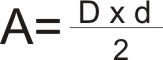Volumen de los Cuerpos Geométricos

     El volumen no es más que el espacio ocupado por un cuerpo. Universalmente se toma como unidad de medida de volúmenes el metro cúbico (m³). Los múltiplos y divisores del m³ se construyen a partir de cubos cuyas aristas sean las unidades de longitud.

     La siguiente tabla muestra la equivalencia de las unidades de volumen.

     Polígonos

     El volumen del Icosaedro y Dodecaedro se calculan con la misma fórmula, por lo tanto se presenta como ejemplo al icosaedro. Conformado por triángulos equiláteros.

     El octaedro si lo observamos bien esta conformado por dos pirámides de con base cuadrada, por lo tanto la fórmula que se aplica es la de la pirámide multiplicando por 2.

     Para el tetraedro también aplica la fórmula de la pirámide.

    

Para calcular un paralelepipedo se aplica el área de la base multiplicada por la altura.

     Para calcular el área de cualquier prisma se debe calcular primero la base y multiplicarla por la altura del prisma.

     Al igual que un tetraedro, el volumen de una pirámide es igual a la tercera parte del producto de la base por su altura.

Para calcular un tronco de piramide, se debe calcular primero sus bases, al igual que un trapecio, tiene una base mayor y una menor.

     En relación a los cuerpos redondos, presentamos tres de ellos.

ÁREA DE FIGURAS GEOMÉTRICAS

ÁREAS

     Muchas veces se tiende a confundir los términos área y superficie, la superficie se refiere a la forma y presenta dos dimensiones. En cuanto al área, esta se refiere al tamaño o la medida de la superficie.
Unidades de superficie
     Son las unidades que se utilizan para expresar las extensiones en dos dimensiones. Se dividen en múltiplos y submúltiplos y su unidad es el m2. En la siguiente tabla podemos observar las diferentes medidas de superficie, útiles para realizar conversiones.

Área de polígonos regulares

Recordemos que un polígono es regular si tiene iguales todos sus lados y todos sus ángulos. Entre los más comunes existen 10, mostraremos las formulas de sólo tres de ellos, ya verán porque.

Triángulo Equilátero

 

A =Bxh/2

         B= Base           

                                     h= Altura                                      

Cuadrado

                                                                              A= L²

 

Los otros polígonos se calculan a través de la misma fórmula, ya que lo que varía entre ellos es el número de lados.

P= Perímetro el perímetro se obtiene de multiplicar la longitud por el número de lados P= LxN

L= Longitud

N= número de lados

Pentágono 

    

Área de Paralelogramos

Existen cuatro tipos de paralelogramos: Cuadrado, rectángulo, rombo y romboide. El cuadrado ya lo tratamos en los polígonos regulares, ya que por poseer todos sus lados y ángulos iguales es un polígono, pero también es un paralelogramo porque posee lados iguales opuestos y paralelos.

Rectángulo

A= B x h

Rombo

ac= Diagonal mayor

bd= Diagonal menor

 Trapecios

Los siguientes trapecios se calculan con la misma fórmula, lo que varía es la figura la posición de las bases y la altura.



Trapecio isósceles

Trapecio rectángulo

Áreas Cirulares 

Círculo

π= 3.1416                                                           A= πxr²

^{r= Radio}

 Sector Circular

 Segmento Círcular

 El área de un segmento círcular se calcula con la fórmula del sector círcular, restandole el área del triángulo

Corona Círcular

A= π x (R^{2 -} r²)

 

Los Cuerpos Geométricos

Una manera sencilla de definir los cuerpos geométricos es, la representación en el plano de las superficies que lo limitan, de tal manera que al doblarlas, puedan formarlo. Los cuerpos geométricos se dividen en dos grupos: Poliedros y Cuerpos redondos.
Dentro de los poliedros tenemos, los regulares, prismas y pirámides. En cuanto a los cuerpos redondos están los: Cilindro, Cono y esfera.
Los Poliedros Regulares: Los poliedros regulares convexos son conocidos con el nombre de sólidos platónicos en honor al filósofo griego Platón (428-347 a.C.). Algunos investigadores asignan el cubo, el tetraedro y el dodecaedro a Pitágoras (siglo IV a.C.) y el octaedro e icosaedro a Theaetetus, un matemático griego que dio la descripción matemático de los poliedros y es posible que fuera el responsable de la demostración de que no existen otros poliedros regulares convexos (415-369 a.C.).

Tetraedro

Cubo o Hexaedro

Octaedro

Dodecaedro

Icosaedro

Los Prismas: Son poliedros limitados por dos polígonos iguales y paralelos cualesquiera llamados bases. Algunos de ellos son:

Prisma base Triángular

Prisma base Cuadrada

Prisma de base Hexagonal

 



Prisma de base Pentagonal

Pirámides: Son poliedros limitados por un polígono cualquiera llamado base y tantos triangulos como lados tiene la base, llamados caras laterales

Pirámide de base Triángular

Pirámide de base Cuadrada

Pirámide de base Pentagonal

Pirámide de base Hexagonal

Pirámide de base Octogonal

Pirámide de base Rectangular

Pirámide Truncada

Cuerpos Redondos: Son los cuerpos geométricos que se generan por la rotación de 360 ª de una figura plana alrededor de su eje. Los más destacados son el Cilindro, el cono y la esfera

Cilindro

Cono

Cono Truncado

Esfera

Para el desarrollo de la esfera existen varios métodos, uno sencillo es el llamado Método de Gore o Policilíndrico. Allí les dejo una imagen del procedimiento.



Para construir la siguiente, como esta en la imagen. Se realizan todos los círculos que vez (7) así como están allí, a la medida que la necesites. Y aquí te dejo un link de un video que explica como armarla.
https://www.youtube.com/watch?v=2QykhjMDKWo



Los cuerpos geométricos en lámparas decorativas El diseñador holandés Edward van Vliet es el creador de las lámparas de ambiente Rontonton para la firma italiana Moroso, que se caracterizan por su cuerpo geométrico tridimensional fabricado con paneles sandwich perforados de plástico y aluminio.

Los cuerpos geométricos en envases El resultado de la forma de la botella proviene de una aplicación de modelos espaciales en el diseño de envases. Estas formas se encuentran en formaciones de rocas, plantas y otras estructuras celulares y son modelos que también pueden ser generados por cálculos matemáticos y geométricos. La forma elemental de los resultados de LH2O son de la intersección de dos cuerpos geométricos: un simple cubo (cuello de la botella y la tapa) y un cubo truncado (empaque).

Los cuerpos geométricos en empaques